Home  ›  what temperature will be needed to produce a pressure of 4.00 atm

what temperature will be needed to produce a pressure of 4.00 atm

Written By 8 Nisan 2022 Cuma Add Comment Edit

The First Law of Thermodynamics

nineteen Adiabatic Processes for an Ideal Gas

Learning Objectives

By the end of this section, you will be able to:

  • Define adiabatic expansion of an platonic gas
  • Demonstrate the qualitative difference betwixt adiabatic and isothermal expansions

When an ideal gas is compressed adiabatically \left(Q=0\right), work is done on it and its temperature increases; in an adiabatic expansion, the gas does work and its temperature drops. Adiabatic compressions really occur in the cylinders of a car, where the compressions of the gas-air mixture take place so chop-chop that there is no time for the mixture to commutation heat with its environment. Nevertheless, because work is washed on the mixture during the compression, its temperature does ascension significantly. In fact, the temperature increases can be and so large that the mixture can explode without the addition of a spark. Such explosions, since they are non timed, make a automobile run poorly—it usually "knocks." Considering ignition temperature rises with the octane of gasoline, one way to overcome this trouble is to utilize a higher-octane gasoline.

Some other interesting adiabatic process is the costless expansion of a gas. (Figure) shows a gas confined by a membrane to 1 side of a two-compartment, thermally insulated container. When the membrane is punctured, gas rushes into the empty side of the container, thereby expanding freely. Considering the gas expands "against a vacuum" \left(p=0\right), it does no work, and because the vessel is thermally insulated, the expansion is adiabatic. With Q=0 and W=0 in the first law, \text{Δ}{E}_{\text{int}}=0, so {E}_{\text{int}}{}_{i}={E}_{\text{int}}{}_{f} for the gratis expansion.

The gas in the left bedroom expands freely into the right chamber when the membrane is punctured.

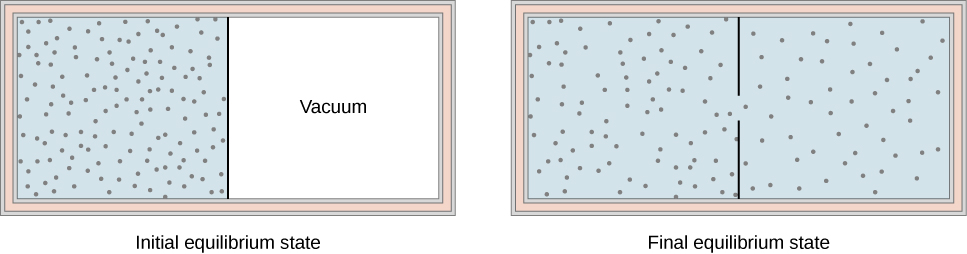
The figure on the left is an illustration of the initial equilibrium state of a container with a partition in the middle dividing it into two chambers. The outer walls are insulated. The chamber on the left is full of gas, indicated by blue shading and many small dots representing the gas molecules. The right chamber is empty. The figure on the right is an illustration of the final equilibrium state of the container. The partition has a hole in it. The entire container, on both sides of the partition, is full of gas, indicated by blue shading and many small dots representing the gas molecules. The dots in the second, final equilibrium state, illustration are less dense than in the first, initial state illustration.

If the gas is ideal, the internal energy depends only on the temperature. Therefore, when an ideal gas expands freely, its temperature does not modify.

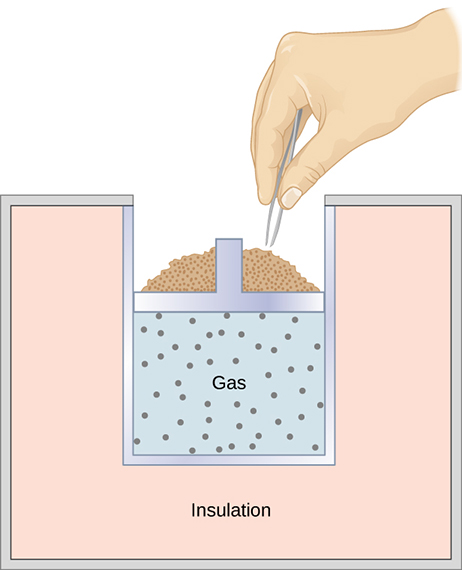
A quasi-static, adiabatic expansion of an platonic gas is represented in (Figure), which shows an insulated cylinder that contains 1 mol of an ideal gas. The gas is made to expand quasi-statically by removing 1 grain of sand at a time from the pinnacle of the piston. When the gas expands past dV, the change in its temperature is dT. The work done by the gas in the expansion is dW=pdV;dQ=0 because the cylinder is insulated; and the change in the internal free energy of the gas is, from (Figure), d{E}_{\text{int}}={C}_{V}dT. Therefore, from the first law,

{C}_{V}dT=0-pdV=\text{−}pdV,

so

dT=-\frac{pdV}{{C}_{V}}.

When sand is removed from the piston one grain at a fourth dimension, the gas expands adiabatically and quasi-statically in the insulated vessel.

The figure is an illustration of a container. The walls and bottom are filled with a thick layer of insulation. The chamber of the container is closed from above by a piston. Inside the chamber is a gas. There is a pile of sand on top of the piston, and a hand with tweezers is removing grains from the pile.

Also, for 1 mol of an ideal gas,

d\left(pV\right)=d\left(RT\right),

then

pdV+Vdp=RdT

and

dT=\frac{pdV+Vdp}{R}.

We now take ii equations for dT. Upon equating them, we discover that

{C}_{V}Vdp+\left({C}_{V}+R\right)pdV=0.

Now, we divide this equation by pV and use {C}_{p}={C}_{V}+R. We are then left with

{C}_{V}\frac{dp}{p}+{C}_{p}\frac{dV}{V}=0,

which becomes

\frac{dp}{p}+\gamma \frac{dV}{V}=0,

where nosotros ascertain \text{γ} as the ratio of the molar heat capacities:

\gamma =\frac{{C}_{p}}{{C}_{V}}.

Thus,

\int \frac{dp}{p}+\gamma \int \frac{dV}{V}=0

and

\text{ln}\phantom{\rule{0.2em}{0ex}}p+\text{γ}\text{ln}\phantom{\rule{0.2em}{0ex}}V=\text{constant}\text{.}

Finally, using \text{ln}\left({A}^{x}\right)=x\text{ln}A\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}AB=\text{ln}\phantom{\rule{0.2em}{0ex}}A+\text{ln}\phantom{\rule{0.2em}{0ex}}B, we tin can write this in the form

p{V}^{\gamma }=\text{constant}\text{.}

This equation is the condition that must be obeyed by an platonic gas in a quasi-static adiabatic process. For example, if an platonic gas makes a quasi-static adiabatic transition from a state with force per unit area and volume {p}_{1} and {V}_{1} to a state with {p}_{2} and {V}_{2}, then it must be true that {p}_{1}{V}_{1}^{\gamma }={p}_{2}{V}_{2}^{\gamma }.

The adiabatic condition of (Effigy) tin can be written in terms of other pairs of thermodynamic variables by combining it with the platonic gas law. In doing this, we notice that

{p}^{1-\gamma }{T}^{\gamma }=\text{constant}

and

T{V}^{\gamma -1}=\text{constant}\text{.}

A reversible adiabatic expansion of an platonic gas is represented on the pV diagram of (Figure). The slope of the bend at whatever signal is

\frac{dp}{dV}=\frac{d}{dV}\left(\frac{\text{constant}}{{V}^{\gamma }}\right)=\text{−}\gamma \frac{p}{V}.

Quasi-static adiabatic and isothermal expansions of an ideal gas.

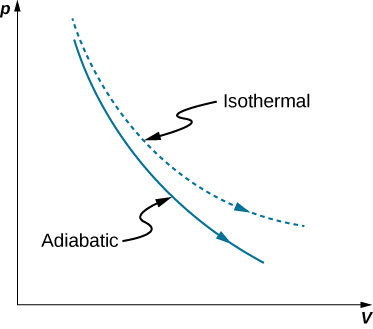
The figure is a plot of pressure, p on the vertical axis as a function of volume, V on the horizontal axis. Two curves are plotted. Both are monotonically decreasing and concave up. One is slightly higher and has a greater curvature. This curve is labeled

The dashed bend shown on this pV diagram represents an isothermal expansion where T (and therefore pV) is abiding. The slope of this curve is useful when we consider the second law of thermodynamics in the side by side chapter. This slope is

\frac{dp}{dV}=\frac{d}{dV}\phantom{\rule{0.2em}{0ex}}\frac{nRT}{V}=-\frac{p}{V}.

Considering \text{γ}>1, the isothermal bend is not as steep every bit that for the adiabatic expansion.

Compression of an Platonic Gas in an Machine Engine Gasoline vapor is injected into the cylinder of an automobile engine when the piston is in its expanded position. The temperature, pressure, and volume of the resulting gas-air mixture are 20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}, 1.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}{\phantom{\rule{0.2em}{0ex}}\text{N/m}}^{2}\text{,} and 240{\phantom{\rule{0.2em}{0ex}}\text{cm}}^{3}, respectively. The mixture is so compressed adiabatically to a volume of 40{\phantom{\rule{0.2em}{0ex}}\text{cm}}^{3}. Annotation that in the actual operation of an auto engine, the compression is non quasi-static, although nosotros are making that assumption here. (a) What are the pressure and temperature of the mixture after the compression? (b) How much work is done by the mixture during the compression?

Strategy Because we are modeling the process as a quasi-static adiabatic compression of an ideal gas, we have p{V}^{\gamma }=\phantom{\rule{0.2em}{0ex}}\text{constant} and pV=nRT. The work needed can so exist evaluated with W={\int }_{{V}_{1}}^{{V}_{2}}pdV.

Solution

  1. For an adiabatic compression we accept

    {p}_{2}={p}_{1}{\left(\frac{{V}_{1}}{{V}_{2}}\right)}^{\gamma },


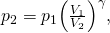
    so after the compression, the pressure of the mixture is

    {p}_{2}=\left(1.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}{\phantom{\rule{0.2em}{0ex}}\text{N/m}}^{2}\right){\left(\frac{240\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}{\phantom{\rule{0.2em}{0ex}}\text{m}}^{3}}{40\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}{\phantom{\rule{0.2em}{0ex}}\text{m}}^{3}}\right)}^{1.40}=1.23\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{6}{\phantom{\rule{0.2em}{0ex}}\text{N/m}}^{2}\text{.}


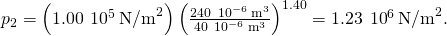
    From the ideal gas constabulary, the temperature of the mixture later the compression is

    \begin{array}{cc}\hfill {T}_{2}& =\left(\frac{{p}_{2}{V}_{2}}{{p}_{1}{V}_{1}}\right){T}_{1}\hfill \\ & =\frac{\left(1.23\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{6}{\phantom{\rule{0.2em}{0ex}}\text{N/m}}^{2}\right)\left(40\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}{\phantom{\rule{0.2em}{0ex}}\text{m}}^{3}\right)}{\left(1.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}{\phantom{\rule{0.2em}{0ex}}\text{N/m}}^{2}\right)\left(240\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}{\phantom{\rule{0.2em}{0ex}}\text{m}}^{3}\right)}·293\phantom{\rule{0.2em}{0ex}}\text{K}\hfill \\ & =600\phantom{\rule{0.2em}{0ex}}\text{K}=328\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}\text{.}\hfill \end{array}

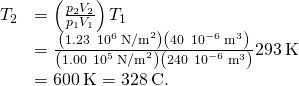
  2. The work done by the mixture during the compression is

    W={\int }_{{V}_{1}}^{{V}_{2}}pdV.


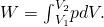
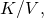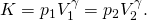    With the adiabatic status of (Figure), we may write p as K\text{/}{V}^{\text{γ}}, where K={p}_{1}{V}_{1}^{\gamma }={p}_{2}{V}_{2}^{\gamma }. The work is therefore

    \begin{array}{cc}\hfill W& \phantom{\rule{0.2em}{0ex}}={\int }_{{V}_{1}}^{{V}_{2}}\frac{K}{{V}^{\gamma }}dV\hfill \\ & \phantom{\rule{0.2em}{0ex}}=\frac{K}{1-\gamma }\left(\frac{1}{{V}_{2}{}^{\gamma -1}}-\frac{1}{{V}_{1}{}^{\gamma -1}}\right)\hfill \\ & =\phantom{\rule{0.2em}{0ex}}\frac{1}{1-\gamma }\left(\frac{{p}_{2}{V}_{2}^{\gamma }}{{V}_{2}{}^{\gamma -1}}-\frac{{p}_{1}{V}_{1}^{\gamma }}{{V}_{1}{}^{\gamma -1}}\right)\hfill \\ & =\phantom{\rule{0.2em}{0ex}}\frac{1}{1-\gamma }\left({p}_{2}{V}_{2}-{p}_{1}{V}_{1}\right)\hfill \\ & \phantom{\rule{0.2em}{0ex}}=\frac{1}{1-1.40}\left[\left(1.23\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{6}\phantom{\rule{0.2em}{0ex}}{\text{N/m}}^{2}\right)\left(40\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}{\text{m}}^{3}\right)\hfill \\ & -\left(1.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}\phantom{\rule{0.2em}{0ex}}{\text{N/m}}^{2}\right)\left(240\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}{\text{m}}^{3}\right)\right]\hfill \\ & \phantom{\rule{0.2em}{0ex}}=-63\phantom{\rule{0.2em}{0ex}}\text{J}\text{.}\hfill \end{array}

Significance The negative sign on the work done indicates that the piston does piece of work on the gas-air mixture. The engine would non piece of work if the gas-air mixture did piece of work on the piston.

Summary

  • A quasi-static adiabatic expansion of an ideal gas produces a steeper pV curve than that of the corresponding isotherm.
  • A realistic expansion can be adiabatic but rarely quasi-static.

Conceptual Questions

Is it possible for \text{γ} to be smaller than unity?

No, it is e'er greater than 1.

Would you look \text{γ} to be larger for a gas or a solid? Explicate.

There is no change in the internal energy of an ideal gas undergoing an isothermal process since the internal free energy depends only on the temperature. Is information technology therefore correct to say that an isothermal process is the same equally an adiabatic process for an ideal gas? Explain your reply.

An adiabatic process has a change in temperature just no heat menstruum. The isothermal process has no change in temperature but has heat period.

Does a gas do any work when it expands adiabatically? If then, what is the source of the energy needed to do this work?

Problems

A monatomic ideal gas undergoes a quasi-static adiabatic expansion in which its volume is doubled. How is the pressure of the gas changed?

pressure level decreased past 0.31 times the original force per unit area

An ideal gas has a pressure level of 0.50 atm and a volume of 10 L. It is compressed adiabatically and quasi-statically until its pressure is three.0 atm and its volume is 2.8 50. Is the gas monatomic, diatomic, or polyatomic?

Pressure level and volume measurements of a dilute gas undergoing a quasi-static adiabatic expansion are shown below. Plot ln p vs. V and determine \text{γ} for this gas from your graph.

P (atm) V (L)
xx.0 ane.0
17.0 i.1
14.0 i.3
eleven.0 1.5
8.0 2.0
5.0 2.6
two.0 5.2
1.0 8.4

The figure is a plot of pressure, p, in atmospheres on the vertical axis as a function of volume, V, in liters on the horizontal axis. The horizontal volume scale runs from 0 to 20, and the vertical pressure scale runs from 0 to 9. The data from the previous table is plotted as points and the equation y equals 8.4372 x to the minus 0.713 power is plotted as a curve. The points all lie on or very close to the curve.

;
\gamma =0.713

An ideal monatomic gas at 300 K expands adiabatically and reversibly to twice its volume. What is its final temperature?

An platonic diatomic gas at eighty K is slowly expanded adiabatically and reversibly to twice its volume. What is its final temperature?

84 Yard

An platonic diatomic gas at eighty K is slowly compressed adiabatically to one-tertiary its original volume. What is its concluding temperature?

Compare the charge in internal energy of an ideal gas for a quasi-static adiabatic expansion with that for a quasi-static isothermal expansion. What happens to the temperature of an ideal gas in an adiabatic expansion?

An adiabatic expansion has less work washed and no oestrus flow, thereby a lower internal energy comparing to an isothermal expansion which has both oestrus flow and work done. Temperature decreases during adiabatic expansion.

The temperature of due north moles of an ideal gas changes from {T}_{1} to {T}_{2} in a quasi-static adiabatic transition. Show that the work done by the gas is given by

W=\frac{nR}{\gamma -1}\left({T}_{1}-{T}_{2}\right).

A dilute gas expands quasi-statically to iii times its initial book. Is the terminal gas pressure greater for an isothermal or an adiabatic expansion? Does your reply depend on whether the gas is monatomic, diatomic, or polyatomic?

Isothermal has a greater final force per unit area and does non depend on the type of gas.

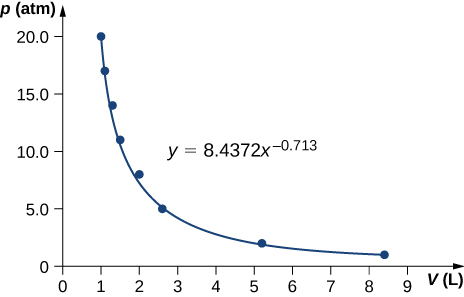
On an adiabatic procedure of an ideal gas force per unit area, volume and temperature modify such that p{V}^{\gamma } is constant with \gamma =5\text{/}3 for monatomic gas such as helium and \gamma =7\text{/}5 for diatomic gas such as hydrogen at room temperature. Use numerical values to plot ii isotherms of ane mol of helium gas using ideal gas law and 2 adiabatic processes mediating betwixt them. Use {T}_{1}=500\phantom{\rule{0.2em}{0ex}}\text{K},\phantom{\rule{0.2em}{0ex}}{V}_{1}=1\phantom{\rule{0.2em}{0ex}}\text{L},\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}{T}_{2}=300\phantom{\rule{0.2em}{0ex}}\text{K} for your plot.

The figure is a plot of pressure, p, in atmospheres on the vertical axis as a function of volume, V, in liters on the horizontal axis. The horizontal, V, axis runs from 1.0 to 2.0. The vertical, p, axis runs from 0 to about 40. Two isotherms are shown. One isotherm is for T equal to 500 K, with the pressure starting at about 40 atmospheres when the volume is 1.0 Liter and decreasing with volume to about 25 atmospheres at 2.0 liters. The second isotherm is for T equal to 300 K, with the pressure starting at about 25 atmospheres when the volume is 1.0 Liter and decreasing with volume to a little over 10 atmospheres at 2.0 liters. A third plot, labeled

Two moles of a monatomic platonic gas such as helium is compressed adiabatically and reversibly from a state (iii atm, 5 Fifty) to a country with pressure iv atm. (a) Observe the volume and temperature of the terminal country. (b) Observe the temperature of the initial state of the gas. (c) Notice the work done by the gas in the procedure. (d) Find the change in internal energy of the gas in the process.

Additional Problems

Consider the process shown below. During steps AB and BC, 3600 J and 2400 J of estrus, respectively, are added to the system. (a) Discover the work done in each of the processes AB, BC, Advertisement, and DC. (b) Find the internal energy alter in processes AB and BC. (c) Observe the internal energy difference between states C and A. (d) Find the total heat added in the ADC process. (eastward) From the information given, tin you find the heat added in procedure AD? Why or why non?

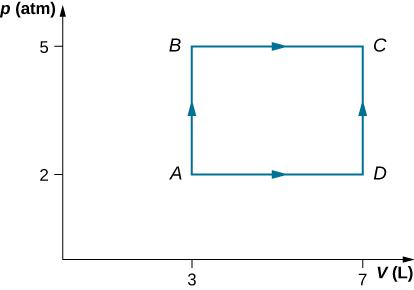
The figure is a plot of pressure, p, in atmospheres on the vertical axis as a function of volume, V, in liters on the horizontal axis. The horizontal volume scale runs from 0 to 7, and the vertical pressure scale runs from 0 to 5. Four points, A, B, C, and D, are labeled on the plot and their pressures and volumes are labeled on the axes. Point A is at volume 3 L, pressure 2 atmospheres. Point B is at volume 3 L, pressure 5 atmospheres. Point C is at volume 7 L, pressure 5 atmospheres. Point D is at volume 7 L, pressure 2 atmospheres. A path goes from A up to B and across to C. Another path goes from A across to D and then up to C.

a. {W}_{AB}=0,{W}_{BC}=2026\phantom{\rule{0.2em}{0ex}}\text{J},{W}_{AD}=810.4\phantom{\rule{0.2em}{0ex}}\text{J},{W}_{DC}=0; b. \text{Δ}{E}_{AB}=3600\phantom{\rule{0.2em}{0ex}}\text{J},\text{Δ}{E}_{BC}=374\phantom{\rule{0.2em}{0ex}}\text{J;} c. \text{Δ}{E}_{AC}=3974\phantom{\rule{0.2em}{0ex}}\text{J}; d. {Q}_{ADC}=4784\phantom{\rule{0.2em}{0ex}}\text{J;} e. No, considering heat was added for both parts Advertizing and DC. There is not enough information to effigy out how much is from each segment of the path.

A car tire contains 0.0380{\phantom{\rule{0.2em}{0ex}}\text{m}}^{3} of air at a pressure of 2.20\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}\phantom{\rule{0.2em}{0ex}}\text{Pa} (virtually 32 psi). How much more than internal free energy does this gas have than the same book has at cipher gauge force per unit area (which is equivalent to normal atmospheric pressure)?

A helium-filled toy airship has a gauge pressure of 0.200 atm and a book of 10.0 L. How much greater is the internal energy of the helium in the balloon than it would be at zero gauge pressure?

300 J

Steam to bulldoze an quondam-fashioned steam locomotive is supplied at a constant approximate pressure level of 1.75\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{6}{\text{N/m}}^{2} (nigh 250 psi) to a piston with a 0.200-1000 radius. (a) By calculating p\text{Δ}V, observe the work done by the steam when the piston moves 0.800 chiliad. Note that this is the cyberspace piece of work output, since gauge pressure level is used. (b) Now observe the amount of work past calculating the force exerted times the distance traveled. Is the answer the aforementioned equally in part (a)?

A hand-driven tire pump has a piston with a 2.50-cm diameter and a maximum stroke of 30.0 cm. (a) How much work do you do in ane stroke if the average approximate force per unit area is 2.4\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}{\phantom{\rule{0.2em}{0ex}}\text{N/m}}^{2} (about 35 psi)? (b) What average force do y'all exert on the piston, neglecting friction and gravitational force?

a. 59.5 J; b. 170 N

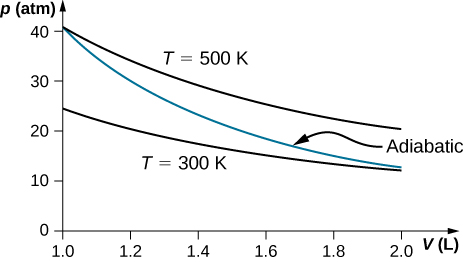
Calculate the net work output of a estrus engine following path ABCDA every bit shown below.

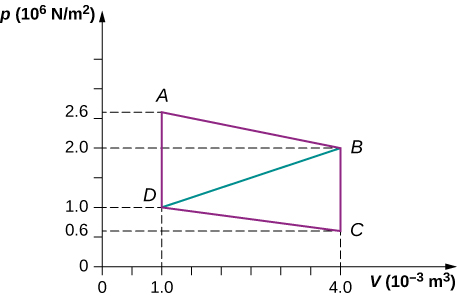
The figure is a plot of pressure, p, in nuits of 10 to the 6 Newtons per meter squared on the vertical axis as a function of volume, V, in 10 to the minus 3 cubic meters on the horizontal axis. The horizontal volume scale runs from 0 to 4, and the vertical pressure scale runs from 0 to about 4. Four points, A, B, C, and D, are labeled on the plot and their pressures and volumes are labeled on the axes. Point A is at volume 1.0 times 10 to the -3 cubic meters, pressure 2.6 times 10 to the 6 Newtons per meter squared. Point B is at volume 4.0 times 10 to the -3 cubic meters, pressure 2.0 times 10 to the 6 Newtons per meter squared. Point C is at volume 4.0 times 10 to the -3 cubic meters, pressure 0.6 times 10 to the 6 Newtons per meter squared. Point D is at volume 1.0 times 10 to the -3 cubic meters, pressure 1.0 times 10 to the 6 Newtons per meter squared. A straight line connects A to B, another straight line B to C, another straight line C to D, and another straight line back to A.

What is the net work output of a heat engine that follows path ABDA in the preceding problem with a straight line from B to D? Why is the work output less than for path ABCDA?

2.4\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{J}

Five moles of a monatomic ideal gas in a cylinder at 27\phantom{\rule{0.2em}{0ex}}\text{°}\text{C} is expanded isothermally from a volume of v Fifty to 10 L. (a) What is the alter in internal energy? (b) How much work was done on the gas in the procedure? (c) How much heat was transferred to the gas?

Four moles of a monatomic platonic gas in a cylinder at 27\phantom{\rule{0.2em}{0ex}}\text{°}\text{C} is expanded at constant pressure equal to 1 atm until its volume doubles. (a) What is the change in internal energy? (b) How much work was washed by the gas in the process? (c) How much rut was transferred to the gas?

a. 15,000 J; b. 10,000 J; c. 25,000 J

Helium gas is cooled from 20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C} to 10\phantom{\rule{0.2em}{0ex}}\text{°}\text{C} by expanding from twoscore atm to one atm. If there is 1.4 mol of helium, (a) What is the final volume of helium? (b) What is the alter in internal energy?

In an adiabatic process, oxygen gas in a container is compressed forth a path that tin can be described past the post-obit pressure in atm as a office of book V, with {V}_{0}=1L: p=\left(3.0\phantom{\rule{0.2em}{0ex}}\text{atm}\right)\left(V\text{/}{V}_{0}{\right)}^{-1.2}. The initial and final volumes during the procedure were ii L and one.5 L, respectively. Detect the corporeality of piece of work done on the gas.

78 J

A cylinder containing three moles of a monatomic platonic gas is heated at a constant force per unit area of 2 atm. The temperature of the gas changes from 300 Grand to 350 K every bit a issue of the expansion. Notice work done (a) on the gas; and (b) by the gas.

A cylinder containing iii moles of nitrogen gas is heated at a constant pressure of 2 atm. The temperature of the gas changes from 300 K to 350 K every bit a result of the expansion. Find work done (a) on the gas, and (b) past the gas by using van der Waals equation of state instead of platonic gas police force.

A cylinder containing three moles of nitrogen gas is heated at a constant pressure of ii atm. a. −1220 J; b. +1220 J

Two moles of a monatomic ideal gas such as oxygen is compressed adiabatically and reversibly from a land (3 atm, 5 L) to a country with a force per unit area of 4 atm. (a) Find the volume and temperature of the final state. (b) Observe the temperature of the initial state. (c) Detect piece of work done by the gas in the process. (d) Find the change in internal free energy in the procedure. Assume {C}_{V}=5R and {C}_{p}={C}_{V}+R for the diatomic ideal gas in the conditions given.

An insulated vessel contains 1.5 moles of argon at 2 atm. The gas initially occupies a volume of 5 Fifty. Every bit a result of the adiabatic expansion the pressure of the gas is reduced to 1 atm. (a) Detect the book and temperature of the final state. (b) Find the temperature of the gas in the initial state. (c) Discover the work done past the gas in the procedure. (d) Find the modify in the internal free energy of the gas in the process.

a. 7.half dozen L, 61.6 One thousand; b. 81.3 Thou; c. 3.63\phantom{\rule{0.2em}{0ex}}\text{L}·\text{atm}=367\phantom{\rule{0.2em}{0ex}}\text{J}; d. −367 J

Challenge Problems

One mole of an ideal gas is initially in a chamber of book 1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}{\phantom{\rule{0.2em}{0ex}}\text{m}}^{3} and at a temperature of 27\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}. (a) How much estrus is captivated past the gas when it slowly expands isothermally to twice its initial volume? (b) Suppose the gas is slowly transformed to the same final land by first decreasing the pressure at constant volume and then expanding information technology isobarically. What is the rut transferred for this case? (c) Calculate the heat transferred when the gas is transformed quasi-statically to the same concluding state by expanding it isobarically, so decreasing its force per unit area at constant volume.

a. 1700 J; b. 1200 J; c. 2400 J

A bullet of mass x yard is traveling horizontally at 200 yard/south when it strikes and embeds in a pendulum bob of mass two.0 kg. (a) How much mechanical energy is dissipated in the collision? (b) Assuming that {C}_{v} for the bob plus bullet is 3R, calculate the temperature increment of the system due to the collision. Take the molecular mass of the system to exist 200 g/mol.

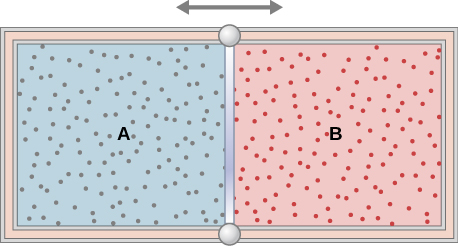
The insulated cylinder shown below is closed at both ends and contains an insulating piston that is free to move on frictionless bearings. The piston divides the sleeping room into two compartments containing gases A and B. Originally, each compartment has a volume of 5.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}{\phantom{\rule{0.2em}{0ex}}\text{m}}^{3} and contains a monatomic platonic gas at a temperature of 0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C} and a pressure of one.0 atm. (a) How many moles of gas are in each compartment? (b) Heat Q is slowly added to A so that it expands and B is compressed until the pressure of both gases is 3.0 atm. Employ the fact that the pinch of B is adiabatic to decide the final volume of both gases. (c) What are their final temperatures? (d) What is the value of Q?

The figure is an illustration of a container with a partition in the middle dividing it into two chambers. A double headed horizontal arrow above the partition indicates that it is moveable The outer walls are insulated. The chamber on the left is labeled with an A, and is full of one gas, indicated by blue shading and many small dots representing the gas molecules. The right chamber is labeled with a B, and is full of a second gas, indicated by red shading and many small dots representing the gas molecules.

a. 2.2 mol; b. {V}_{A}=2.6\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}{\text{m}}^{3}, {V}_{B}=7.4\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}{\text{m}}^{3}; c. {T}_{A}=1220\phantom{\rule{0.2em}{0ex}}\text{K},{T}_{B}=430\phantom{\rule{0.2em}{0ex}}\text{K}; d. 30,500 J

howellgrapt1953.blogspot.com

Source: https://opentextbc.ca/universityphysicsv2openstax/chapter/adiabatic-processes-for-an-ideal-gas/

0 Response to "what temperature will be needed to produce a pressure of 4.00 atm"

Yorum Gönder

Kaydol: Kayıt Yorumları (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel